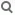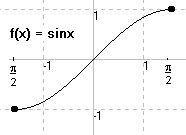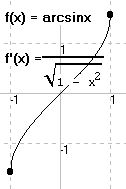Umkehrfunktionen: Teil II
Aufgabe 4: Berechne die Umkehrfunktionen! Skizziere dabei Funktion und Umkehrfunktion!
4
a) f(x) = -x + 1 D = R
5 f
2x - 3 2
b) f(x) = —————— D = R \{-}
2 - 7x f 7
2
c) f(x) = x - 2x - 1 D = [1,∞]
f
2x - 3
d) f(x) =2e + 1 D = R
f
2 2
e) f(x) = -ln(2 - 3x) D = (-∞, -)
3 f 3
1 —————
-\/2 - x
2
f) f(x) = e D = (-∞,2]
f
x + 1
——————
5x - 5
g) f(x) = e D = R \ {1}
f
1 2
h) f(x) = - -x + x + 2 D = [1; ∞)
2 f
2x+1
i) f(x) = —————— D = (-1,0)
x(x+1) f
LösungenBeweis: Den Nachweis, dass f‾'(y) existiert, wollen wir den Mathematikprofis überlassen. Dies vorausgesetzt können wir f‾'(y) folgendermaßen aus der Kettenregel
h(x) = f(g(x) =» h'(x) = f'(g(x)·g'(x) berechnen:
- -' -' 1
x= f(f(x)) =» 1 = f (f(x))·f'(x) =» f (f(x)) = —————
f'(x)
Analog leiten wir her:
- - -' -' 1
x = f(f(x)) =» 1 = f'(f(x))·f (x) =» f (x) = ————————
f'(f‾(x))
Beispiele 11:
2 - -
a) f(x) = x x ε [0, ∞] f(x) = \/x
-' 1 1
f'(x) = 2x f (x) = ————————— = ——————
f'(f‾(x)) -
2· \/x
x -
b) f(x) = e f(x) = lnx
x -' 1 1 1
f'(x) = e f (x) = ————————— = ———— = -
f'(f‾(x)) lnx x
e
c) (siehe Beispiel 9)
π π -
f(x) = tanx D = (- -, -) f(x) = arctanx, x ε R
f 2 2
2 - 1 1 1
f'(x) = 1 + tan x f'(x) = ——————————— = ———————————————— = ——————
f'(arctanx) 2 2
1 + tan (arctanx) 1 + x
Polynomdivision liefert die geometrische Reihe für f'(x):
2 2 4 6 8
f'(x) = 1 : (1 + x ) = 1 - x + x - x + x + ...
2
-(1 + x )
————————
2
- x
2 4
-(-x - x )
—————————
4
x
...
Die Stammfunktion ist dann unter Berücksichtigung von arctan0 = 0:
1 3 1 5 1 7 1 9
f(x) = arctanx = x - -x + -x - -x + -x - ...
3 5 7 9
π π
Da tan45° = tan - = 1, ist arctan 1 = -. Somit
4 4
π 1 1 1 1
- = 1 - - + - - - + - - (Gottfried Wilhelm Leibniz, 1646-1716)
4 3 5 7 9
Als Leibniz diese Formel entdeckte, schwärmte er "numero
deus impari gaudet" ("Gott freut sich der ungeraden Zahlen").
Die Konvergenz dieser Reihe ist allerdings sehr langsam.
Heutzutage berechnet man π auf Milliarden von Stellen
"mörderisch" schnell. ![]() Pi
Pi
n n - 1
f(x) = x =» f'(x) = n·x für n ε Z.
Schränken wir den Definitionsbereich auf D = (0,∞) ein, so existiert
f
1
-
- n
die Umkehrfunktion f(x) = x (x ε (0,∞]). Diese hat die Ableitung
1 1 n-1
f'(x) = ———————— = ———————————— , da f'(u) = nu
- - n-1
f'(f(x)) n·(f(x))
n-1 -(n-1) 1-n 1
- ——— —————— ——— - - 1
1 1 1 n 1 n 1 n 1 n
f'(x) = ——————————— = ——————— = -x = -x = -x = -x
1 n-1 n n n n
- n-1 ———
n n
n·(x ) n·(x )
m 1 1
- - -
n m n n m
Nach der Kettenregel folgt dann für f(x) = x = (x ) = u für u = x
1 1 1 m
- - 1 - - 1 m·(- - 1) + (m - 1) - - 1
1 n 1 m n m-1 m n m n
f'(x) = -u ·u' = -(x ) ·mx = -x = -x
n n n n
a a - 1
Damit ist auch für a ε Q gezeigt: f(x) = x =» f'(x) = ax
1 1
- - -
- 2 1 2 1
Zum Beispiel: f(x) = \/x = x =» f'(x) = -x = —————
2 -
2 \/x
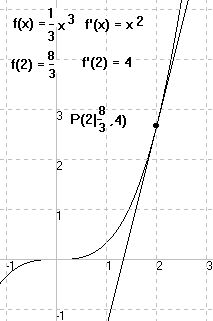
Aufgabe 5:
- - 1 3 1
a) Berechne f(2) und f'(2) für f(x) = ——x + -x
27 3
-
Hinweis: f kann man nicht in geschlossener Form angeben.
Verwende aber f(3) = 2
b) Berechne mit Hilfe der Umkehrfunktion die Ableitung der
3-
Funktion f(x) = \/x x ε [0,∞)
-
c) Berechne die Ableitung der Umkehrfunktion f(x) = arcsinx von
π π
f(x) = sinx D = [- -; -] (Nur so ist sin umkehrbar!)
f 2 2
-
Zeichne f und f
Lösungen
Vorbemerkung zu den folgenden Sätzen: Für die Exponentialfunktion f: x -» ex und die Logarithmusfunktion f‾: x -» ln(x) gilt:
a b a+b
e ·e = e und ln(u·v) = ln(u) + ln(v), d.h.
- - -
f(a)·f(b) = f(a+b) und f(u·v) = f(u) + f(v).
—————————————————————————
a
e a - b u
—— = e und ln- = ln(u) - ln(v), d.h.
b v
e
f(a) - u - -
———— = f(a - b) und f(-) = f(u) - f(v)
f(b) v
Diese Eigenschaften bedingen nach den folgenden Sätzen einander.
Satz 8
Gilt für alle a,b ε Df: f(a)·f(b) = f(a+b), so folgt für alle u,v ε D f‾: f‾(u·v) = f‾(u) + f‾(v).
Beweis: Seien u,v ε Df‾.
Setzte a = f‾(u) und b = f‾(v). Dann ist nach der Basisgleichung u = f(a) und v = f(b). Setzten wir nun die Gleichung f(a)·f(b) = f(a+b) voraus, dann folgt:
f‾(u·v) = f‾(f(a)·f(b)) = f‾(f(a+b)) = a + b = f‾(u) + f‾(v)
Satz 9
Gilt für alle für alle u,v ε Df‾: f‾(u·v) = f‾(u) + f‾(v), so folgt für alle a,b ε Df: f(a)·f(b) = f(a+b)
Beweis: Seien a,b ε Df.
Setzte u = f(a) und v = f(b). Dann ist nach der Basisgleichung a = f‾(u) und b = f‾(v). Setzten wir nun die Gleichung f‾(u·v) = f‾(u) + f‾(v) voraus, dann folgt:
f(a+b) = f(f‾(u) + f‾(v)) = f(f‾(u·v)) = u·v = f(a)·f(b)
Die Subtraktion ist die Umkehrung der Addition, die Division die Umkehrung der Multiplikation. Dies spiegelt sich im folgenden Satz:
Satz 10
I Gilt für alle a,b ε Df: f(a)·f(b) = f(a + b), dann gilt für alle a,b ε D f mit f(b) ≠ 0: f(a)/f(b) = f(a - b).
II Gilt für alle für alle u,v ε D f‾: f‾(u·v) = f‾(u) + f‾(v), dann gilt für alle u,v ε Df‾ mit v ≠ 0: f‾(u/v) = f‾(u) - f‾(v).
Beweis: Setzten wir jeweils die angebebene Beziehung voraus, dann folgt:
I f(a - b)·f(b) = f(a - b + b) = f(a) =» f(a)/f(b) = f(a - b)
II f‾(u/v)·f(v) = f‾(u/v·v) = f‾(u) =» f‾(u)/f‾(v) = f‾(u-v)
Bemerkung: Die Funktionalgleichung f(a)·f(b) = f(a+b)
charakterisiert die Exponentialfunktion nach folgendem
Satz:
Satz 11 Eine stetige Funktion f mit der Eigenschaft
f(u)·f(v) = f(u + v) für alle u,v ε R
mit b = f(1) » 0 ist von der Form:
x
f(x) = b für x ε R.
Beweis: Wir zeigen den Satz zuerst für die Zahl 0, dann für alle natürliche Zahlen,
für alle rationalen positiven und negativen Zahlen und schließlich für alle reelle Zahlen.
Es ist f(0) ≠ 0, sonst wäre b = f(1) = f(0 + 1) = f(0)·f(1) = 0.
f(0)
Dann folgt: f(0) = f(0 + 0) = f(0)·f(0), somit f(0) = ———— = 1.
f(0)
n
f(n) = f(1 + 1 + 1 + ... + 1) = f(1)·f(1)·...·f(1) = b für n ε N
(n mal) (n mal)
n m
Für n,m ε N und x = - ist f(n) = f(m·x) = f(x)·f(x)·...·f(x) = (f(x))
m
(m mal)
1 1 n
- - -
m n m m
Also ist f(x) = f(n) = (b ) = b , also
x
f(x) = b für rationales positives x.
1
Da aus 1 = f(0) = f(x - x) = f(x)·f(-x) folgt: f(-x) = ————, gilt
f(x)
1 1 -x
f(-x) = ———— = —— = b auch für negatives rationales -x.
f(x) x
b
Aus Stetigkeitsgründen gilt der Satz auch für alle reellen x ε R.
Für die folgenden Überlegungen werden Sätze der höheren Mathematik benötigt.
Satz: Das stetige Bild eines kompakten Raumes ist wieder
kompakt.
Satz: Das stetige Bild eines zusammenhängenden Raumes
ist wieder zusammenhängend.
Daraus folgt für reellwertige Funktionen:
Satz: Das stetige Bild eines abgeschlossenen Intervalls ist
ein abgeschlossenes Intervall, d.h.
eine stetige Funktion nimmt auf einem abgeschlossenen
Intervall des Maximum und Minimum und jeden Zwischenwert
an.
Satz 12 Die Umkehrfunktion einer stetigen monotonen
Funktion ist stetig.
Beweis siehe Wilhelm Maak: Differential- und Integralrechnung. S.58.
Satz 13 Ist f auf einem Intervall stetig und umkehrbar, dann ist f auf diesem Intervall streng monoton.|
Nicht möglich bei einer 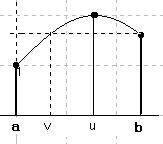
|
Beweis: Sei a,b ε Df mit a « b.
Wir setzen noch ohne Einschränkung f(a) « f(b)
voraus. Falls dies nicht der Fall ist, können wir
(- f) betrachten. |
Lösung zu Aufgabe 1: Gegeben ist die Umrechnungsformel:
T = f(t) = 9/5t + 32 (t: °Celsius, T: °Fahrenheit).
Man muß "mal 9/5" und "plus 32" in der umgekehrten Reihenfolge rückgängig machen. Also ist
t = f‾(T) = 5/9(T - 32). Zum Beispiel: 86 °Fahrenheit = f‾(86) °Celsius = 30° Celsius.
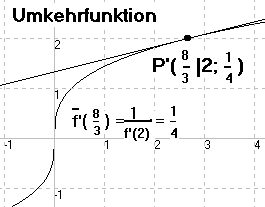
Lösung zu Aufgabe 2: Das Schaubild der Umkehrfunktion erhält man einfach durch Vertauschen der Abszissen- und Ordinatenwerte. (Absizze = x-Achse, Ordinate = y-Achse)
|
|
| Lösung zu Aufgabe 3: Die Umkehrabbildung von |
P(x|y|z) -» P'(x + 4|y + 5|z + 3) ist P(x|y|z) -» P'(x - 4|y - 5|z - 3) |
Lösung zu Aufgabe 4:
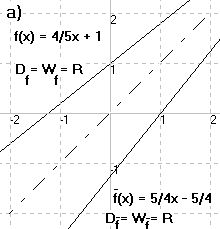
|
|
Stets: W = D , W = D
f - - f
f f
zu a)
4
f(x) = -x + 1
5
- 5
f(x) = -(x - 1)
4
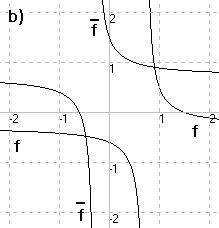
zu b)
2x - 3 2
f(x) = —————— (x ≠ -)
2 - 7x 7
- 5x + 3 2
f(x)=—————— (x≠- -)
7x + 2 7
|
|
|
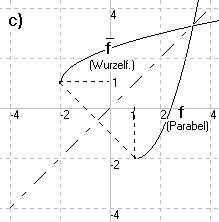
zu c)
2
f(x) = x - 2x - 1
2
= (x - 1) - 2
(x ≤ 1)
- —————
f(x) = 1 + \/x + 2
(x ≥ 2)
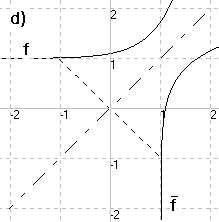
zu d)
2x - 3
f(x) = 2e + 1
(x ε R)
- 1 x-1 3
f(x) = -ln——— + -
2 2 2
(x » 1)
|
|
|
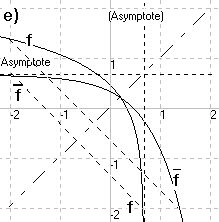
zu e)
2
f(x) = -ln(2-3x)
3
2
(x « -)
3
3x
——
- 2 1 2
f(x) = - - -e
3 2
(x ε R)
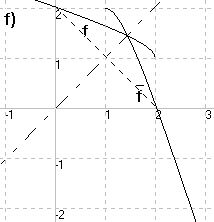
zu f) 1 —————
-\/2 - x
2
f(x) = e
(x ≥ 2)
- 2
f(x) = 2 - 4(lnx)
(x ≥ 1)
|
|
|
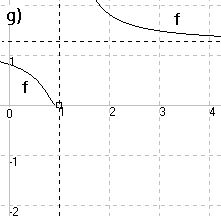
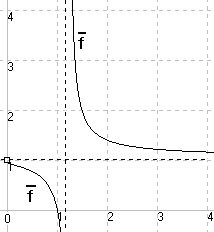
zu g)
x + 1
——————
5x - 5
f(x) = e
( x ≠ 1)
waagr. Asymtote
0,2
y = e
5lnx + 1
f(x) = ————————
5lnx - 1
0,2
(x ε (0,∞) \ {e })
in Q(0|1) senkrechte
Tangente
|
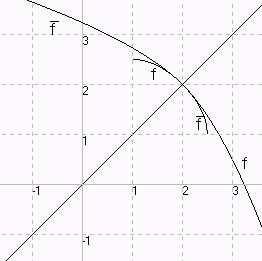
|
zu h)
1 2
y = - -x + x + 2 (x≤1 und y≥2,5)
2
1 2
=»- -x + x + 2 - y = 0
2
Auflösen nach x:
——————
x = - 1 ± \/5 - 2y
"-" entfällt, da x≥1.
Vertauschen von x und y ergibt:
—————
y = - 1 + \/5 - 2x (x≥2,5 und y≤1)
——————
Somit: f(x) = - 1 + \/5 - 2x (x≥2,5)
|
|
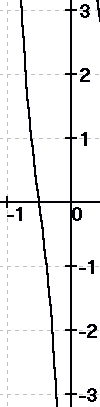
|
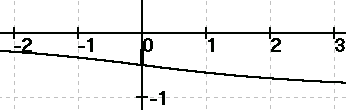
|
zu i)
2x+1
f(x) = ——————
x(x+1)
Hier: D =(-1;0)
f
W = (-∞;∞)
f
(Zeichnung alle Zweige)
—————
2
- 2-x-\/x + 4
f(x) = ——————————— für x≠0
2x
- 1
f(0) = - - (hebbar)
2
D- = (-∞;∞)
f
W- = (-1;0)
f
|
Hinweis zu den Umformungen: Vielleicht hast Du bei a) bzw. g)
-3 - 5x -1 - 5lnx
das Ergebnis ——————— bzw. ————————— . Auch dieses Ergebnis ist richtig!
-2 - 7x 1 - 5lnx
Man vermeidet jedoch zu viele Minuszeichen, indem man mit (-1) erweitert.
a - b b - a a - b
Allgemein gilt: ————— = —————. Sonderfall: ————— = - 1
c - d d - c b - a
Lösung zu Aufgabe 5:
a)
1 3 1 1 2 1
f(x) = ——x + -x f'(x) = -x + -
27 3 9 3
4
f(3) = 2 f'(3) = -
3
- - 1 - 1 1 3
f(2) = 3 f'(x) = ———————— f'(2) = ———————— = ————— = -
- - 4
f'(f(x)) f'(f(2)) f'(3)
- 1 - 1 3
oder f'(b) = ————— für a = 3 und b = f(3) = 2 =» f'(2) = ————— = -
f'(a) f'(3) 4
- 3-
b) Die gegebene Funktion f(x) = \/x ist die Umkehrfunktion von
3 -
f(x) = x (Verübergehend vertauschen wir f und f.)
2 - 1 1
Mit f'(x) = 3x folgt f'(x) = ———————— = ———————
- 3- 2
f'(f(x)) 3(\/x)
3- 1
Also ist für f(x) = \/x die Ableitung f'(x) = ——————
3- 2
3(\/x)
1 2
- ——
3 1 3
Probe: f(x) = x =» f'(x) = -x (Probe stimmt!)
3
|
π π
c) f(x) = sinx, D = [- -, -]
f 2 2
—————————
f'(x) = cosx = \/1 - sin2x
(Eine dieser "wunderbaren" Umformungen der
Mathematik. Für diejenigen, die nicht draufkommen
(also, wir alle), ist es ein "übler Trick".)
(Hier wichtig: Für x ε D ist cosx ≤ 0)
f
-
f(x) = arcsinx, D = W = [-1,1]
- f
f
- 1
f'(x) = ———————————
f'(arcsinx)
1
= ————————————————_ (siehe "Trick")
———————————————
\/1 - sin2arcsinx
1
= ————————
——————
\/1 - x2
π π
x ε (- -, -)
2 2
|