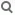Joachim Mohr Mathematik Musik

Umkehrfunktionen

Vorbemerkungen

Hier handelt es sich um ein ganz allgemeines mathematisches Thema. Deshalb ist hier nicht nur von Funktionen die Rede (i.a. meint man damit Funktionen, deren Argumente und Werte reelle Zahlen sind) sondern von Abbildungen (Zuordnungen im allgemeinsten Sinn).
Hier bedeutet Funktion und Abbildung dasselbe, nämlich eine Zuordnung f von einer Menge A in eine zweite Menge B, geschrieben:

f: A → B
f: x |→ f(x)
A ist die Definitionsmenge von f, meist D_f geschrieben und - das ist hier besonders wichtig - gehört mit zur Angabe von f. Die Menge, in der die Werte von f sind, ist die "Zielmenge" B (oder "Bildmenge"), - bei reellwertigen Funktionen immer ℝ. B ist zu unterscheiden von der Wertemenge W_f von f. Hier sind nur die Elemente von B erfasst, die auch wirklich als Funktionswerte angenommen werden.

Beispiel:	f: R → R	f: R → [-1;1]	f: R → [-1;1]
	f: x → sin(x)	f: x → sin(x)	f: y → sin(y)
Dieselbe Funktion		(Zielmenge kleiner)	(Variable y statt x)

Definitionsmenge von f ist D_f = R und die Werte von f sind in R. Hier ist leicht ersichtlich, da -1 ≤ sin(x) ≤ 1, dass die Werte sin(x) alle reelle Zahlen im abgeschlossenen Intervall [-1;1] annehmen, mehr Werte aber nicht. Der Wertebereich von f ist hier also W_f = [-1;1].

Bemerkung: Zwei Funktionen f und g sind gleich, d.h. g = f, wenn gilt:

D _f = D _g und
f(x) = g(x) für alle x ε D _f = D _g.

Achtung: In manchen Lehrbüchern wird bei der Gleichheit von Funktionen noch verlangt, dass die Zielmengen (Bildmengen) gleich sind. Bei dieser strengen Definition ist eine Funktion genau dann umkehrbar, wenn sie bijektiv (= injektiv+surjektiv) ist.

(Surjektiv bedeutet: Die Zielmenge ist der Wertebereich).

Im folgenden genügt für die Umkehrbarkeit nur die Injektivität, da hier die Umkehrfunktion von f auf der Wertemenge W_f definiert wird und f automatisch eine surjektive Funktion von D_f aug W_f ist.

Definition:
f‾ heißt Umkehrfunktion zu f, wenn sie f "rückgängig macht":
Genauer: wenn für alle x ε D_f gilt:

Wenn y= f(x), dann x = f‾(y) (Basisgleichung),
d.h. f‾(f(x))=x.

Hier wird die Umkehrfunktion mit f‾ ("f quer") bezeichnet. Umkehrfunktionen existieren nicht immer.

Es ist klar, dass f‾ auf dem Wertebereich W_f definiert sein muss, d.h. D_f‾ = W_f

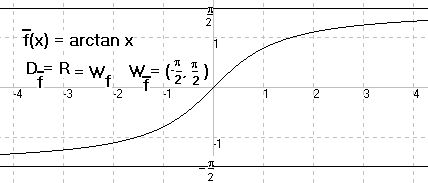
Beispiel 1

            2
  f: x |-> x  Definitionsbereich z.B. D = [0;2]
                                       f
               Wertebereich W = [0;4] .
                             f

                                       2
  Zu jedem x ε D  kann man y = f(x) = x   angeben.
                f
                                                        2
  Zum Beispiel ist für x = 1,5 speziell y = f(1,5) = 1,5 = 2,25.

  Umgekehrt kann man zu jedem y ε W  das Argument x ε [0;2]
                                   f
              2
  finden mit x = y. Nehmen wir zum Beispiel y = 2,2801.

                                            2
  Nun wird eine Zahl x ε [0;2] gesucht mit x = 2,2801.

                            ——————
  Das ist bekanntlich x = \/2,2801 = 1,51. Allgemein finden wir

                                              -
  zu jedem y ε W   das passende x durch x = \/y.
                f

  Die Umkehrfunktion von f ist also

  -            -
  f: y |-> = \/y,  y ε W = [0;4].
                        f

                 ——
                  2            - 2
  Hier:        \/x = x  und (\/y)  = y.

               -                   -
  Allgemein:   f(f(x)) = x   und f(f(y)) = y.

Damit ist die Umkehrfunktion der Quadratfunktion die Wurzelfunktion:

            -          -
            f: y |-> \/y mit y ε [0;4].

Die allgemein Quadratfunktion f mit f(x)=x² (xεR) ist nicht umkehrbar und hat deshalb auch keine Umkehrfunktion, da zum Beispiel 4=f(x) also 4=x² keine eindeutige Lösung hat. Es gibt zwei Lösungen: x=2 und x=-2.

Um die Quadratfunktion als umkehrbare Funktion darzustellen mußten wir im obigen Deispiel den Definitionsbereich einschränken:

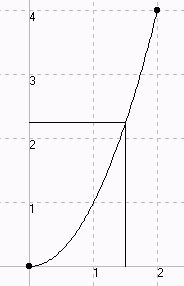
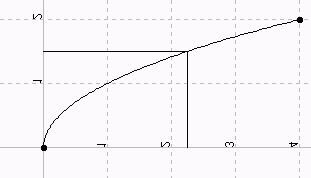
Wir wenden uns nun dem Schaubild der Umkehrfunktion zu.

Im Schaubild suchen wir zu gegebenem y-Wert auf der Hochachse den zugehörigen auf der x-Achse. Das Schaubild der Umkehrfunktion ist also schon mit dem Schaubild der Funktion f gezeichnet.

Nur: Für gewöhnlich suchen wir zu gegebenem Wert auf der Rechtsachse den zugehörigen Wert auf der Hochachse. Bei der Umkehrfunktion hier ist es umgekehrt.

Wenn's denn unbedingt sein muss:
Drehe das Schaubild um 90° nach rechts und spiegle es dann an der Rechtsachse:

oder was dasselbe ist

Spiegle das Schaubild an der ersten Winkelhalbierenden
(Beides Mal wird bewirkt: Hoch- und Rechtsachse werden vertauscht.)

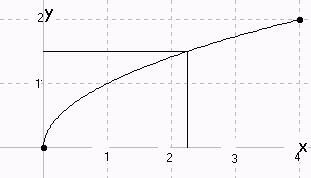
Du willst sicher jetzt noch die Rechts- als x- und die Hoch- als y-Achse bezeichnen. Auch das ist möglich. Vertauschen wir x und y. Dann lautet die Umkehrfunktion zu f: x |→ f(x) = x², x ε [0;2]

    -          -
    f: x |-> \/x     x ε [0;4]

    D  = [0;4]  = W    W  = [0;2] = D
     f‾            f    f‾           f

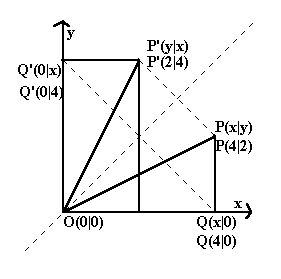
Bemerkung zur Spiegelung an der 1. Winkelhalbierenden:

Die x- Achse wird auf die y-Achse gespiegelt.

               Q(x|0) auf Q'(0|x)
zum Beispiel   Q(4|0) auf Q'(0|4)

Das Dreieck   0(0|0)Q (x|0)P (x|y) auf
              0(0|0)Q'(0|x)P'(y|x)

zum Beispiel  0(0|0)Q( 4|0)P (4|2) auf
              0(0|0)Q'(0|4)P'(2|4)

Die x- und y-Werte werden also vertauscht.

               P(x|y) auf P'(y|x)
zum Beispiel   P(4|2) auf P'(2|4)

Aufgabe 1 Die Umrechnung der Temperatur von der Celsius-Skala in die Fahrenheitskala ist f(t) = 9/5t + 32 (t: °Celsius, f(t): °Fahrenheit).

Zum Beispiel ist 20° Celsius = f(20) °Fahrenheit = 68 °Fahrenheit.

Gib die Umkehrfunktion an und rechne 86 °Fahrenheit in °Celsius um!

Lösung

Aufgabe 2:

                                          1 3  1
Skizziere das Schaubild von f mit f(x) = ——x + -x
                                         10    5

mit Hilfe der Werte f(0), f(1), f(2) und f(3)!

                                                -
Skizziere dann das Schaubild der Umkehrfunktion f!

Lösung

Beispiel 2 Eine Permutation

  Funktion p(1)=1   Umkehrfunktion: p‾(1)=1
           p(2)=5                   p‾(2)=4
           p(3)=4                   p‾(3)=5
           p(4)=2                   p‾(4)=3
           p(5)=3                   p‾(5)=2

Die Funktion p und ihre Umkehrfunktion p‾ sind auf der endlichen Menge {1,2,3,4,5} definiert.
Eine umkehrbare Funktion, deren Wertemenge identisch mit ihrer Definitionsmenge ist, nennt man -vor allem, wenn sie auf einer endlichen Menge definiert ist- auch Permutation.

Beispiel 3 (Das Inverse bezüglich der Multiplikation modulo 11)

Gesucht ist für alle x ε {1, 2, 3, ..., 10} der Wert p(x) so, dass x·p(x) = 1 mod 11,
d. h. p(x) soll das Inverse von x bezüglich der Multiplikation modulo 11 sein.
(Da 11 Primzahl ist, ist das möglich.)

           p(1)=1,   da 1·1   = 1
           p(2)=6,   da 2·6   = 11   + 1, also 2·6   = 1 mod 11
           p(3)=4,   da 3·4   = 11   + 1, also 3·4   = 1 mod 11
           p(4)=3,   da 4·3   = 11   + 1, also 4·3   = 1 mod 11
           p(5)=9,   da 5·9   = 4·11 + 1, also 5·9   = 1 mod 11
           p(6)=2,   da 6·2   = 11   + 1, also 6·2   = 1 mod 11
           p(7)=8,   da 7·8   = 5·11 + 1, also 7·8   = 1 mod 11
           p(8)=7,   da 8·7   = 5·11 + 1, also 8·7   = 1 mod 11
           p(9)=5,   da 9·5   = 4·11 + 1, also 9·5   = 1 mod 11
           p(10)=10, da 10·10 = 9·11 + 1, also 10·10 = 1 mod 11

  Funktion p(1)=1   Umkehrfunktion: p‾(1)=1
           p(2)=6                   p‾(2)=6
           p(3)=4                   p‾(3)=4
           p(4)=3                   p‾(4)=3
           p(5)=9                   p‾(5)=9
           p(6)=2                   p‾(6)=2
           p(7)=8                   p‾(7)=8
           p(8)=7                   p‾(8)=7
           p(9)=5                   p‾(9)=5
           p(10)=10                 p‾(10)=10

Die Permutation p ist auf {1,2,3,4,5,6,7,8,9,10} definiert und identisch mit seiner Umkehrfunktion p‾.

In Delphi kann man die Permutation p und Umkehrfunktion p_ von p folgendermaßen programmieren.

function p(n: integer): integer;
begin
  Case n of 0: result := 5; //Definitionsbereich {1,2,...,f(0)}
            1: result := 1;
            2: result := 5;
            3: result := 4;
            4: result := 2;
            5: result := 3;
    else raise Exception.CreateFmt(
      	      '%d liegt nicht im Definitionsbereich',[n]);
  End;
end;

function p_(n: integer): integer; //Umkehrfunktion von p
  var i:integer;
begin
  for i := 1 to f(0) do //f(0)=Maximalwert
    if p(i) = n then Begin //p(i) = n <=> p_(n) = i (Basisgleichung)
      result := i;
      exit;
    End;
end;

Effizienter ist das Speichern von p und der Umkehrfunktion q in zwei Arrays. Die Umkehrfunktion wird dann mit folgender Prozedur ein- für allemal berechnet:

   var p,q: array[1..max] of integer;
   ...
   procedure speichere_invers_von_p_in_q;
     var u, v: integer;
   begin
     for u := 1 to max do
       for v := 1 to max do
         if p[u] = v then q[v] := u; //Basisgleichung
   end;

Bei reellwertigen Funktionen werden die Umkehrfunktionen durch ausgeklügelte Verfahren der höheren Mathematik berechnet, die 3. Wurzel z.B. mittels des Newton-Verfahren.

function rt3(a: real): real;
   const eps = 1E-17; //Real hat 15-16 sign. Stellen
   var old: real;
begin
  if a = 0 then Begin
    result := 0;
    exit;
  End;
  result := abs(a)/3;
  repeat
    old := result;
    result := (2*result + abs(a)/sqr(result))/3;
    //für f(x) = x^3 - a ist x(n+1)=1/3*(2*xn-a/xn^2)
  until  abs(result - old) < result*eps; //relativer Fehler
  if a < 0 then result := - result; //Hier: sqrt3(-64) = -4 etc.
end;

(Gegen-)Beispiel 4

Die folgende auf {1,2,3,4,5} definierte Funktion ist nicht umkehrbar!

  Funktion p(1)=1   Nicht umkehrbar, da p(2)=p(5) und daher
                     -
           p(2)=3   "p(3)" nicht eindeutig.

           p(3)=4

           p(4)=2

           p(5)=3

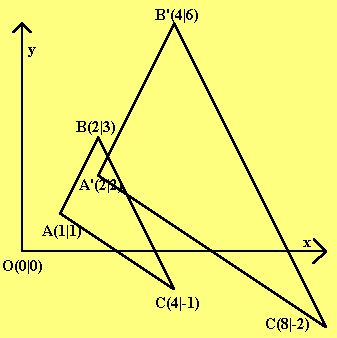
Beispiel 5 (zentrische Streckung)

Ein Beispiel für eine umkehrbare Funktion
aus der Geometrie ist die zentrische Streckung
von O(0|0) aus mit dem Faktor 2.

  Abbildung (im Sinne von Funktion)

         2     2
 f:     R  -> R

    P(x|y) → P'(2x|2y)

  Umkehrabbildung (Umkehrfunktion)

    -      2      2
    f:    R  →  R
                   x y
      P(x|y) → P'(-|-)
                   2 2

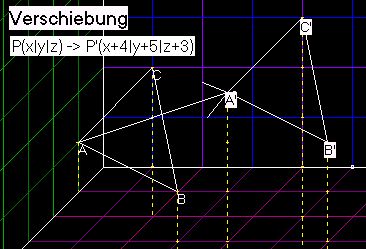
Aufgabe 3 Bestimme die Umkehrabbildung
einer Verschiebung um den Vektor

            4
      →
      a = ( 5 )

            3

Zum Beispiel: A(1|0|1) → A'(5|5|4)

              B(5|4|2) → B'(9|9|5)

              C(2|2|3) → C'(6|7|6)

Lösung

Wenden wir uns wieder der Theorie zu:

Satz 1

Die Umkehrfunktion von f ist eindeutig definiert. (Deshalb ist die Bezeichnung f‾ für die Umkehrfunktion überhaupt erst gerechtfertigt.)

Beweis: Seien g und h Umkehrfunktionen von f. Das bedeutet:

(1) Der Definitionsbereich von g und h ist W_f.
(2) g(f(x)) = x für alle x ε D_f.
(3) h(f(x)) = x für alle x ε D_f.

Um die Gleichheit der Funktionen g und h zu zeigen, müssen wir nachweisen:

g(y) = h(y) für alle y ε W_f.
Nachweis: Sei y ε W_f. Dann existiert x ε D _f mit y = f(x). Nach (2) und (3) folgt: g(f(x)) = x = h(f(x)).
Also g(y) = h(y).

Satz 2
Die Umkehrfunktion von f‾ ist f,

          =
     d.h. f = f .

Beweis: Die Basisgleichung

y = f(x) <=> x = f‾(y)

zeigt schon diese Symmetrie.

Führen wir den Beweis ganz formal, so müssen wir uns nur die Definition der Umkehrfunktion genau anschauen:
h ist Umkehrfunktion von f‾, wenn für alle y = f(x) ε W_f, dem Definitionsbereich von f‾, mit x ε D_f gilt:
h(f‾(y)) = y bzw. h(f‾(f(x))) = f(x)
Mit der Beziehung f‾(f(x)) = x folgt:
h(x) = f(x) für alle x ε D_f.

Somit: Die Funktion f erfüllt alle Bedingungen, um Umkehrfunktion von f‾ zu sein.

Zusammenfassung
Für die Funktion f und ihre Umkehrfunktion f‾ gilt stets:

(A)  D_f‾ = W_f     und    W_f‾ = D_f

(B)  y = f(x) <=> x=f‾(y), x ε D_f, y ε D _f‾     (Basisgleichung)

(C)   f‾(f(x)) = x für alle x ε D_f

(D)  f(f‾(y)) = y für alle y ε D_f‾

Dabei ist nur aus psychologischen Gründen ein Mal die Variable mit x, das andere Mal mit y bezeichnet.

Logisch ist kein Unterschied zwischen "für alle x gilt Aussage(x)" und "für alle y gilt Aussage(y)".

Spezialfälle

          2
a)  f(x)=x       D = [0, ∞]    W = [0, ∞]
                  f             f

                   -       -
    Umkehrfunktion f(x) =\/x

    Die Wurzelfunktion lernt man als erste nicht triviale Umkehrfunktion kennen.

       -
    "\/a ist die Zahl (nicht negativ!), deren Quadrat a ist."

    Wir prüfen die Bedingungen (B) bis (D):

              2            -
    (B)  y = x   <=> x = \/y

          ——
           2
    (C) \/x  = x

           - 2
    (D) (\/y)  = y

             x
b)  f(x) = 10   D = R   W = (0, ∞)
                 f       f

                   -
    Umkehrfunktion f(x) = lg x       x > 0

    "lg a ist die Zahl, mit der man 10 potenzieren muss, um a zu erhalten."

              x
    (B) y = 10  <=> x = lg y

             x
    (C) lg 10  = x     Wissen alle (bis auf ein paar wenige)!

          lgx
    (D) 10    =  x     Weiß keiner (bis auf ein paar wenige)!

            x
c)  f(x) = e   D = R   W = (0, ∞)
                f       f

                   -
    Umkehrfunktion f(x) = ln x       x > 0

    "ln a ist die Zahl, mit der man e potenzieren muss, um a zu erhalten."

             x
    (B) y = e  <=> x = ln y

            x
    (C) ln e  = x      Wissen alle (bis auf endlich viele)!

         lnx
    (D) e    =  x      Weiß keiner (bis auf endlich viele)!

(Gegen-)Beispiel 6

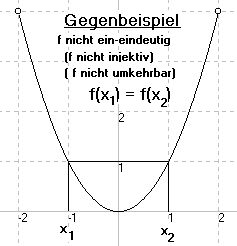
f: x |→ x² Definitionsbereich D_f = [-2;2].
Hätte diese Funktion eine Umkehrfunktion f‾, dann müsste gelten:
f‾(f(1)) = 1 und f‾(f(-1)) = -1. D.H. f‾(1) = 1 und f‾(1) = -1.
Das ist ein Widerspruch! f besitzt hier keine Umkehrfunktion!
Das liegt daran, dass f(-1) = f(1) ist.
Damit eine Umkehrfunktion existiert, muss man also für alle x₁, x ₂ ε D_f fordern:

x₁≠x₂ => f(x₁) ≠ f(x₂) oder, was dasselbe bedeutet (logisch die Kontraposition) f(x₁) = f(x₂) => x₁ = x₂ (Hier Betonung auf der Implikation "=>")

Wir kommen nun zu der Frage: Wann ist eine Funktion umkehrbar?
Beachte hierzu auch Satz 6

Definition

f heißt ein-eindeutig (injektiv), wenn gilt: f(x₁) = f(x ₂) => x₁ = x₂ (*)

Die Implikation (*) kann auch ersetzt werden durch ihre Kontraposition x₁ ≠ x₂ => f(x₁) ≠ f(x ₂). Die folgende Definition ist dann gleichwertig:

Definition

f heißt ein-eindeutig (injektiv), wenn gilt: f(x₁) ≠ f(x ₂) für alle x₁ ≠ x₂

In der Logik nennt man eine Wenn-dann-Konstruktion Implikation .

Die Kontraposition von "Wenn A, dann B" ist "Wenn nicht B, dann nicht A".

Die Kontraposition von "Wenn nicht A, dann nicht B" ist "Wenn B, dann A".

Jeweils beide Implikationen sind äquivalent, d.h. ist die eine gültig, dann auch die andere.

Satz 3
Eine ein-eindeutige Funktion ist umkehrbar,
d.h. besitzt eine Umkehrfunktion f‾ mit D_f‾ = W_f.

Beweis: Für alle y ε W_f existiert genau ein x ε D_f mit y = f(x). Die Funktion f‾, definiert durch f‾(y) = x, falls y = f(x), ist also wohldefiniert und es gilt offensichtlich die Bedingung für die Umkehrfunktion f‾(f(x)) =x für alle x ε D_f .

Definition:

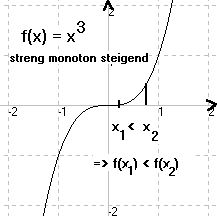
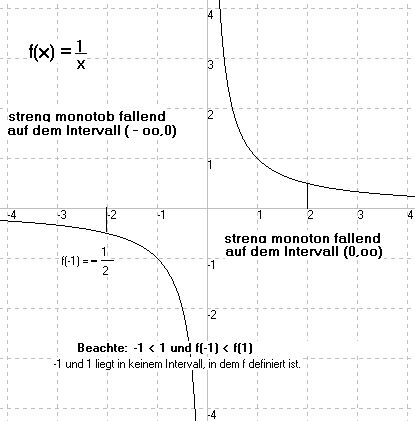
Eine Funktion f heißt streng monoton steigend (wachsend), wenn gilt:
aus x₁ < x₂ folgt f(x₁) < f(x ₂), (hier < :"kleiner als")

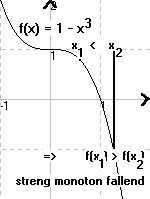
sie heißt streng monoton fallend, wenn gilt:
aus x₁ < x₂ folgt f(x₁) > f(x ₂).

Bei monotonen Funktionen wird stillschweigend vorausgesetzt, dass der Monotoniebereich ein Intervall ist.

Ein offenes Intervall in R ist zum Beispiel (-2,2) oder (0, ∞), ein abgeschlossenes [-2,2] und ein halboffenes (- ∞,0].
Intervalle sind "zusammenhängend", d.h. mit zwei Punkten sind auch alle Punkte dazwischen im Intervall.

Der Nachweis der Monotonie mit Hilfe der Definition ist häufig zu kompliziert, mit Satz 5 jedoch einfach. Zuvor kommen wir auf einen wichtigen Satz zu unserem Thema zu sprechen.

Satz 4
Jede streng monotone Funktion ist umkehrbar.

Beweis: Bei streng monotonen Funktionen gilt für alle x₁ ≠ x₂ ε D_f: f(x ₁) ≠ f(x₂), da die Funktionswerte ja größer bzw. kleiner werden.

Folgender Satz ist einleuchtend, aber in aller Strenge gar nicht so einfach zu beweisen (man benötigt dazu den "Mittelwertsatz", eine Folgerung des "Satzes von Rolle"):

Satz 5
Die Funktion f sei auf einem Intervall definiert und dort differenzierbar. Dann gilt:
Ist f'(x) > 0 bis auf endlich viele Ausnahmen auf endlichen Intervallen, dann ist die Funktion streng monoton steigend, also umkehrbar.

Dasselbe gilt für f'(x) < 0 und streng monoton fallend.

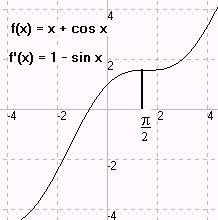
f'(x) > 0 bis auf endlich viele Ausnahmen auf endlichen Intervallen hört sich kompliziert an, bedeutet aber zum Beispiel: auf dem Intervall [-1000,1000] ist f'(x) > 0 bis auf ein paar Ausnahmen, bei denen f'(x) = 0 ist."

Unendlich viele Ausnahmen sind auch erlaubt. Zum Beispiel ist bei f(x) = x + cos(x) die Ableitung f'(x) = 1 - sin(x) > 0 mit Ausnahme der Werte, für die sin(x) = 1 ist, d.h. für die x= π/2+2k·π für k ε Z ist.

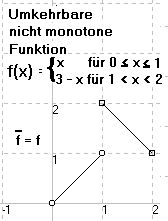
Der Umkehrschluss gilt jedoch nicht. Es gibt umkehrbare reelle Funktion, die nicht monoton sind. (Diese sind zwangsläufig unstetig. Siehe Satz 13)

Im Beispiel hier ist etwa:
f(1,2) = 1,8 und f(1,8) = 1,2, also f(f(1,2)) = 1,2
Das gilt für alle x ε D_f: f(f(x)) = x, d.h. f‾ = f

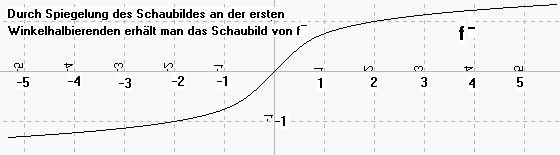
Beispiel 7

f: R → R mit f(x) = x⁵ +x. Wie man leicht nachrechnet ist f'(x)=5x⁴ +1 > 0, also f streng monoton steigend und daher umkehrbar.

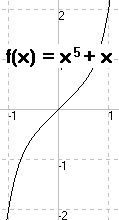
Aus	f(1) = 2	f(0,5) = 0,53125	f(0,9) = 1,49049
folgt umgekehrt:	f‾(2)=1;	f‾(0,53125) = 0,5	f‾(1,49049) = 0,9.

Hier kann man aber nicht jeden Wert f‾(x) exakt angeben, obwohl er ja existieren muss. Nährungsweise kann man jedoch jeden Funktionswert f‾(x) beliebig genau angeben. Zum Beispiel wurde mit dem Newtonverfahren berechnet:f‾(3) = 1,133. Zu ungenau?
Bitte sehr: f‾(3) = 1,13299756588506526672114163428853237981652602772707928311183326069440650817835.

Beispiel 8

f: R → R mit f(x) = x + sin(x). Wie man leicht nachrechnet ist f'(x)=1 + cos(x).

Da -1 < cosx < 1 für alle x ε R mit Ausnahme cos(π) = -1, cos(±3π) = -1, cos(±5π) = -1, ... ist f'(x) > 0 für alle x ε R mit den Ausnahmen f'(±π) = 0, f'(±3π) = 0, ....
Also ist f umkehrbar.

Unendlich oft ist f'(x) = 0. Trotzdem ist f umkehrbar.
Aufgabe: Berechne f‾(6)!
Lösung:
Wir suchen das x mit f(x) = 6, d.h. wir müssen folgende Gleichung lösen: x+ sin(x) - 6 =0. Das ist elementar nicht lösbar. Mit dem Newtonverfahren erhalten wir: x = 6,141355. Somit ist ungefähr f‾(6) = 6,141355.

Dass man die Werte von Umkehrfunktionen oft nur näherungsweise berechnen kann, kennen wir schon von der Quadratfunktion, ist also gar nichts Neues.

Beispiel 9

                          π  π
   f(x) = tan x   D = ( - -, -) W = R
                   f      2  2   f

             1                            2
   f'(x) = ————— oder auch f'(x) = 1 + tan x, da
              2
           cos x

                2       2
     1       sin x + cos x      2
   ————— = ——————————————— = tan x + 1
      2           2
   cos x       cos x

Stets ist f'(x) > 0. Also ist f auf D  streng monoton
                                     f
steigend und somit umkehrbar. Die Umkehrfunktion heißt

                   arctan.

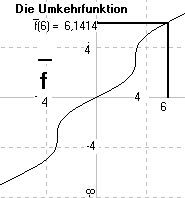
Das Wichtigste: Berechnung der Umkehrfunktion.

Wie berechnet man nun die Umkehrfunktion x → f‾(x) der Funktion x → f(x)?

Wie wir gesehen haben, ist das oft nur näherungsweise möglich.

Lässt sich aber y = f(x) nach x auflösen, dann haben wir die Umkehrfunktion x=f‾(y) als "geschlossene Form" vor uns. Vertauschen wir noch die Variablen x und y, so erhalten wir y = f‾(x) in gewohnter Form.

Wenn wir die Umkehrfunktion so berechnen, brauchen wir vorher gar nicht beweisen, dass die Funktion umkehrbar ist. Dies folgt automatisch nach folgendem Satz:

Satz 6: Kann man y = f(x) nach x ε D_f eindeutig auflösen, dann ist f umkehrbar.

Beweis: Nach Satz 3 ist zu zeigen, dass f unter der genannten Voraussetzung ein-eindeutig ist. Das ist offensichtlich: Lösen wir y = f(x ₁) = f(x ₂) nach x₁ bzw. x₂ auf, so erhalten wir:

x ₁ lässt sich eindeutig aus y berechnen.

x ₂ lässt sich eindeutig aus y berechnen.

eindeutig heißt: x ₁ = x ₂

Also gilt unter der genannten Voraussetzung: Aus f(x₁) = f(x ₂) folgt x₁ = x₂.

Beispiele zur Berechnung der Umkehrfunktion!

. Wenn nichts angegeben ist, ist der Definitionsbereich von f der maximale Definitionsbereich.

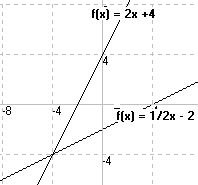
a) f(x) = 2x + 4.

                         1
Lösung: y= 2x + 4 => x = - y - 2.
                         2

        Vertauschen von x und y ergibt:

            -      1
        y = f(x) = -x -2
                   2

        Damit ist auch bewiesen: f ist umkehrbar.

D  = W  = R        W = D  = R
 f    -             f   -
      f                 f

           x + 1                   1
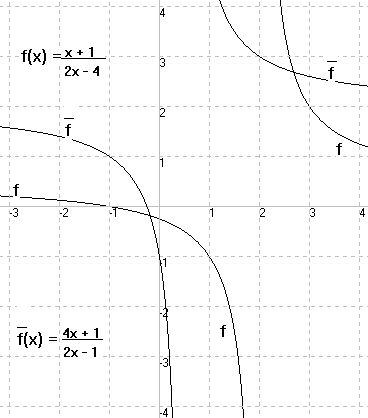
b) f(x) = ——————     Asymptote y = -
          2x - 4                   2

                     (wichtig für W )
                                   f
            x + 1
Lösung: y= ——————
           2x - 4

        =>  2xy - 4y = x + 1

        => x(2y - 1) = 4y + 1

               4y + 1
        => x = ——————
               2y - 1

        Vertauschen von x und y ergibt:

            -      4x + 1
        y = f(x) = ——————
                   2x - 1

       Damit ist auch bewiesen:

       f ist umkehrbar.

                                  1
D = W  = R \ {2}    W = D  = R \ {-}
 f   -               f   -        2
     f                   f

           2
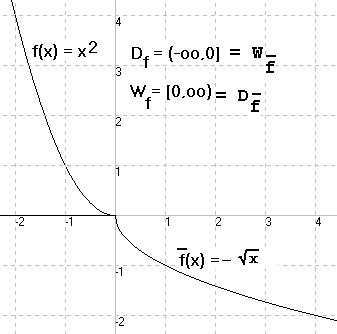
c) f(x) = x     x ε [-∞; 0]

   Im angegebenen Intervall ist f streng  

   monoton fallend, also umkehrbar.

        2
   y = x  ist eindeutig nach

   x ε [- ∞;0] auflösbar:

           -
   x = - \/y

   Vertauschen von x und y ergibt:

                  -
   y = f(x) = - \/x

                         ——
           -              2
  Beachte: f(f(x)) = - \/x  = - |x| = x

           für x < 0  und

            -           - 2
          f(f(x)) = (-\/x)  = x für x > 0

Bemerkung:

                           x für x ≥ 0
Nach Definition ist |x| = {             .
                           -x für x < 0

zum Beispiel: |5| = 5 und |-5| = -(-5) = 5.

                      ——
                       2
Also ist für x < 0  \/x  = |x| = -x,

               ————
                  2      ——
zum Beispiel \/(-5 ) = \/25 = |-5| = -(-5), nämlich 5.

Weiter